Từ một bài toán trong SGK đến các bài toán thi HSG

January 24, 2008

Trong SGK hình học lớp 9 có bài toán sau đây:

Bài toán 1:

         Cho đường tròn (O; R) và một điểm M cố định không nằm trên đường tròn. Qua M kẻ hai đường thẳng. Đường thẳng thứ nhất cắt (O) tại A và B, đường thẳng thứ hai cắt (O) tại C và D. Chứng minh MA.MB = MC.MD

Chứng minh bài toán này không khó bằng cách xét hai trường hợp M nằm ngoài và nằm trong đường tròn (O). Trong mỗi trường hợp chứng minh tam giác MAC và tamg giác MCD đồng dạng, từ đó ta suy ra kết quả cần chứng minh.

Qua bài toán này ta có  thể chứng minh bài toán sau:

Bài toán 2:

       Nếu M không nằm trên đường tròn (O; R), một đường thẳng thay đổi qua M và cắt (O) tại A và B. Khi đó tích MA. MB không đổi và bằng |OM^2 - R^2|

 Chứng minh bài toán 2 chỉ cần vẽ đường thẳng qua M và O cắt (O) tại C, D. Sau đó chứng minh tương tự  bài toán 1 ta được kết quả.

Bài toán 2 cho ta một ý tưởng để giải các bài toán về họ đường tròn đi qua một điểm cố định. Ta cùng xét các bài toán sau:

Bài toán 3 ( Năng Khiếu 2004 – 2005 Chuyên toán) Cho  đường tròn (O) và một điểm A khác O nằm trong đường tròn. Một đường thẳng thay đổi qua A nhưng không đi qua O cắt (O) tại M và N. Chứng minh rằng đường tròn ngoại tiếp tam giác OMN luôn đi qua một điểm cố định khác O.

21.png

Gọi P là giao điểm của đường tròn ngoại tiếp tam giác OMN và tia đối của tia AO. Ta có AP.AO = AM.AN \Rightarrow AP = \dfrac{AM.AN}{AO} không đổi vì A và (O) cố định. Hơn nữa P thuộc tia đối của tia AO cố định nên P là điểm cố định.

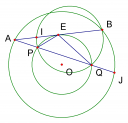
Bài toán 4:  (NK 2006 – 2007 Chuyên toán) Cho đường tròn (O), AB là một dây cung cố định và E là trung điểm của AB. Một đường thẳng thay đổi qua A cắt đường tròn tâm O bán kính OE tại P và Q. Chứng minh rằng tích AP. AQ không đổi và đường tròn ngoại tiếp tam giác BPQ luôn đi qua một điểm cố định.

 31.png

 Vì E là trung điểm của AB nên OE vuông góc với AB, suy ra AB là tiếp tuyến của (O; OE). Ta chứng minh được AP.AQ = AE^2=\dfrac{AB^2}{4} không đổi.

Gọi I là giao điểm của đường tròn ngoại tiếp tam giác BPQ và AB. Khi đó ta có: AI.AB = AP.AQ \Rightarrow AI = \dfrac{AP.AQ}{AB} không đổi. Suy ra I là điểm cố định.

 Bài toán 5: (HSG Q. Tân Bình 2005 – 2006) Từ điểm A nằm ngoài đường tròn (O) vẽ các tuyến ABC (B, C thuộc (O)). Chứng minh rằng khi cát tuyến thay đổi thì tâm đường tròn ngoại tiếp tam giác OBC luôn thuộc một đường thẳng cố định.

41.png

Gọi E là giao điểm của đường tròn ngoại tiếp tam giác OBC và AO. Tương tự như hai bài trên ta chứng minh được E là điểm cố định. Từ đó suy ra tâm đường tròn ngoại tiếp tam giác OBC luôn thuộc đường trung trực của OE.

Bài tập

Bài 1: Cho đường  tròn (O) và đường thẳng d không cắt (O). M là một điểm thay đổi trên d, từ M vẽ hai tiếp tuyến MA và MB đến (O) (A, B là hai tiếp điểm). Chứng minh AB luôn đi qua một điểm cố định.

Bài 2:

Cho đường tròn (O) và một điểm S cố định nằm ngoài đường tròn. AB là đường kính thay đổi. SA, SB cắt (O) tại C và D.

a) Chứng minh đường tròn ngoại tiếp tam giác SAB luôn đi qua một điểm cố định.

b) Chứng minh CD luôn đi qua một điểm cố định.

Bài 3: Cho 3 điểm  C, A, B thẳng hàng và được xếp theo thứ tự đó. Một đường tròn (O) thay đổi luôn đi qua A và B. CP, CQ là các tiếp tuyến của (O) (P, Q là tiếp điểm). Chứng minh rằng:

a)  P, Q luôn thuộc một đường tròn cố định.

b) Trung điểm M của PQ luôn thuộc một đường tròn cố định.

Leave a Comment » | Toán 09, Toán 10 | Tagged: , | Permalink
Posted by vulalach